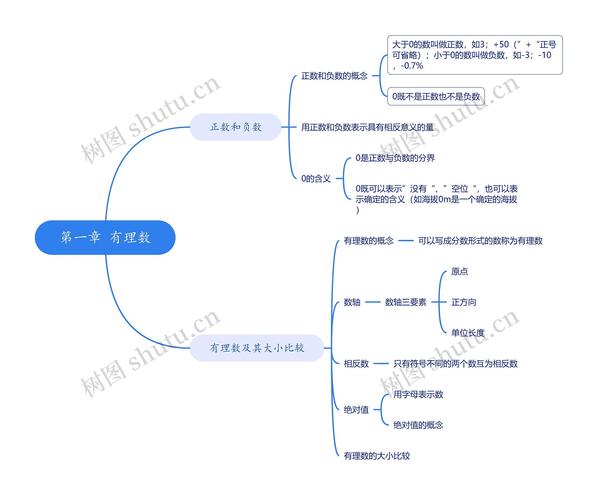
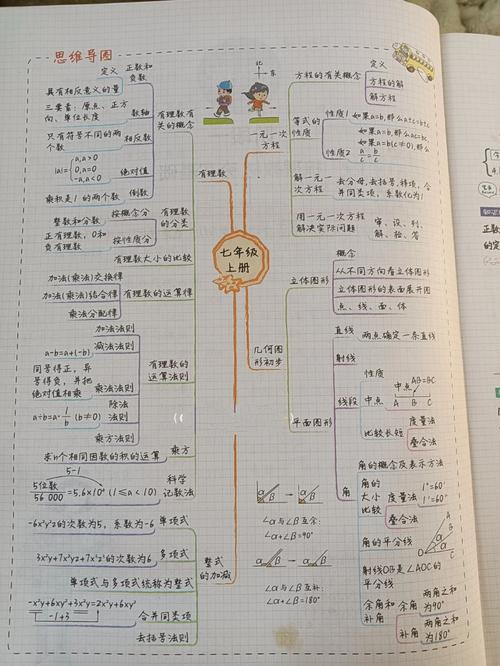
初中数学第一章——网络图
在初中数学的学习过程中,我们常常会发现许多知识点之间并不是孤立存在的,而是在整个数学体系中有着密切的联系,网络图作为一种图论中的概念,可以帮助我们更好地理解和掌握这些知识点之间的关系,从而为我们的数学学习提供一种新的视角,本文将通过网络图的方式,帮助你理解初中数学第一章的核心内容——代数、几何和函数之间的联系。
网络图的基本概念
我们需要明确什么是网络图,网络图是一种将数学中的不同概念或知识点用图论中的节点和边来表示的模型,每个节点代表一个知识点,边则代表这两个知识点之间的联系或依赖关系,通过网络图,我们可以更直观地理解这些知识点之间的关系,以及它们在整体数学体系中的作用。
在初中数学第一章中,我们主要学习代数、几何和函数的内容,为了更好地理解这些内容之间的关系,我们可以将它们绘制成一个网络图,代数中的方程和几何中的图形之间就有一种直接的联系,函数又可以看作是代数和几何之间的桥梁。
代数与几何的网络图
在代数中,我们学习了一元一次方程、二元一次方程、一元二次方程等,这些方程都可以通过网络图来表示它们之间的关系,一元一次方程可以看作是一个节点,而二元一次方程则可以看作是由它引出的另一个节点,这说明代数中的方程之间存在一定的联系,通过解方程可以逐步求解。
同样地,在几何中,我们学习了点、线、面、体等基本概念,这些概念之间也存在着密切的关系,点可以看作是线的起点,线可以看作是面的边界,面可以看作是体的组成部分,体则可以看作是面的构成,通过将这些概念绘制成网络图,我们可以更好地理解它们之间的联系。
代数与函数的网络图
在代数中,函数是代数的核心内容之一,函数可以看作是一个特殊的方程,它描述了两个变量之间的关系,通过将函数与代数中的方程绘制成网络图,我们可以更直观地理解函数的性质,比如函数的定义域、值域、单调性、对称性等。
函数还与几何中的图形紧密相连,函数图像可以看作是函数在坐标系中的表现形式,通过将函数与几何中的图形绘制成网络图,我们可以更好地理解函数的图像特征,比如函数的增减趋势、极值点、渐近线等。
几何与函数的网络图
在几何中,我们学习了点、线、面、体等基本概念,以及它们之间的关系,这些概念之间的关系可以用网络图来表示,点可以看作是线的起点,线可以看作是面的边界,面可以看作是体的组成部分,体则可以看作是面的构成。
函数与几何中的图形紧密相连,函数可以看作是几何图形的函数表达式,而几何图形也可以看作是函数的图像,通过将函数与几何中的图形绘制成网络图,我们可以更直观地理解函数与几何之间的联系。
网络图的应用
网络图的概念在初中数学的学习过程中具有重要的应用价值,网络图可以帮助我们更好地理解数学知识之间的联系,从而提高我们的学习效率,网络图还可以帮助我们进行知识点的复习和巩固,尤其是对于刚入门的学生来说,网络图可以帮助他们更好地记忆和理解知识点。
网络图还可以帮助我们进行数学题的分析和解答,当我们面对一个数学题时,可以将问题中的各个知识点绘制成网络图,从而更直观地理解问题的结构和解题思路。
通过将初中数学第一章的内容绘制成网络图,我们可以更好地理解代数、几何和函数之间的联系,网络图不仅能够帮助我们提高学习效率,还能帮助我们更好地掌握数学知识,我们鼓励大家在学习过程中多尝试网络图的应用,从而更深入地理解数学的奥秘。
如果你对网络图还有其他疑问,欢迎随时提问!